1 To The 4th Power
Exponents
The exponent of a number says how many times to utilise the number in a multiplication.

In 8two the "two" says to employ viii twice in a multiplication,
then eight2 = 8 × 8 = 64
In words: 82 could be called "viii to the power 2" or "8 to the second ability", or simply "8 squared"
Exponents are as well called Powers or Indices.
Some more examples:
Example: 5three = 5 × 5 × five = 125
- In words: 5iii could be chosen "five to the 3rd ability", "five to the power 3" or simply "5 cubed"
Example: 24 = 2 × ii × 2 × 2 = xvi
- In words: 24 could be called "2 to the fourth power" or "2 to the power four" or only "ii to the 4th"
Exponents brand it easier to write and apply many multiplications
Instance: 9half dozen is easier to write and read than 9 × nine × nine × 9 × nine × 9
Y'all tin can multiply any number past itself as many times as you want using exponents.
Effort here:
algebra/images/exponent-calc.js
So in general:
| an tells you to multiply a by itself, so there are n of those a's: | 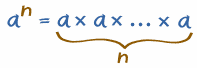 |
Another Way of Writing It
Sometimes people use the ^ symbol (above the 6 on your keyboard), every bit it is easy to type.
Example: two^4 is the aforementioned as ii4
- two^4 = 2 × 2 × 2 × 2 = 16
Negative Exponents
Negative? What could be the opposite of multiplying? Dividing!
So nosotros split by the number each time, which is the same equally multiplying past 1 number
Example: 8-1 = i viii = 0.125
We can continue on like this:
Example: v-3 = 1 5 × 1 five × 1 5 = 0.008
Just it is often easier to do information technology this way:
5-3 could likewise exist calculated like:
1 5 × 5 × 5 = 1 53 = 1 125 = 0.008
Negative? Flip the Positive!
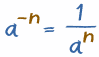 | That last instance showed an easier way to handle negative exponents:
|
More Examples:
| Negative Exponent | Reciprocal of Positive Exponent | Reply | ||
|---|---|---|---|---|
| four-2 | = | 1 / 42 | = | one/16 = 0.0625 |
| 10-three | = | one / 103 | = | ane/i,000 = 0.001 |
| (-2)-three | = | ane / (-ii)3 | = | ane/(-eight) = -0.125 |
What if the Exponent is 1, or 0?
| 1 | If the exponent is 1, then you just have the number itself (example ix1 = 9) | |
| 0 | If the exponent is 0, then you lot become 1 (example 90 = ane) | |
| But what virtually 00 ? It could be either i or 0, and and then people say it is "indeterminate". |
Information technology All Makes Sense
If you wait at that table, you volition run into that positive, cypher or negative exponents are really role of the aforementioned (fairly simple) blueprint:
| Example: Powers of 5 | |||
|---|---|---|---|
| .. etc.. |  | ||
| vtwo | 5 × five | 25 | |
| 51 | 5 | 5 | |
| five0 | ane | 1 | |
| 5-1 | i 5 | 0.2 | |
| 5-2 | 1 5 × 1 5 | 0.04 | |
| .. etc.. | |||
Be Careful Virtually Grouping
To avoid confusion, use parentheses () in cases like this:
| With () : | (−ii)2 = (−two) × (−two) = iv |
| Without () : | −22 = −(ii2) = −(ii × two) = −four |
| With () : | (ab)ii = ab × ab |
| Without () : | ab2 = a × (b)2 = a × b × b |
305, 1679, 306, 1680, 1077, 1681, 1078, 1079, 3863, 3864
1 To The 4th Power,
Source: https://www.mathsisfun.com/exponent.html
Posted by: profittconowitied.blogspot.com


0 Response to "1 To The 4th Power"
Post a Comment